|
Teorie |

|

|
Sarcina limita a unei fundatii de suprafata poate fi definita in functie de valoarea maxima de incarcare pentru care in niciun punct al subsolului nu se ajunge la conditia de rupere (metoda lui Frolich), sau in functie de valoarea sarcinii, mai mare decat precedenta, pentru care fenomenul de ruptura daca este extins la un volum mare al solului (metoda lui Prandtl si urmatorii).
Prandtl a studiat problema de ruptura a unui semispatiu elastic datorata efectului unei sarcini aplicate pe suprafeta sa cu referire la otel, caracterizand rezistenta la forfecare cu o ecuatie de tipul:
|
(1-1) |
valida si pentru terenuri.
Ipotezele si conditiile introduse de Prandtl sunt:
| • | Material fara greutate si deci g=0 |
| • | Comportament rigid-plastic |
| • | Rezistenta la forfecare estimabila cu t=c + s ´ tgj |
| • | Sarcina uniforma, verticala aplicata pe o fasie de lungimea infinita si de latime 2b (stare de deformatie plana) |
| • | Tensiuni tangentiale nule la contactul dintre fasia de sarcina si suprafata limita a semispatiului. |
La forfecare se verifica si plasticizarea materialului dintre suprafetele limita ale semispatiului si suprafetele GFBCD.
In triunghiul AEB forfecarea se realizeaza in functie de doua familii de segmente rectilinii si inclinate la 45°+j/2 fata de orizontala.
In zonele ABF si EBC forfecarea se produce de-a lungul a doua familii de linii, una constituita din segmente rectilinii care trec prin punctele A si E si o alta de arcuri din familia de spirale logaritmice.
Polii acestora sunt punctele A si E. In triunghiurile AFG si ECD ruptura se realizeaza pe segmente inclinate la ±(45°+ j/2) in raport cu verticala.
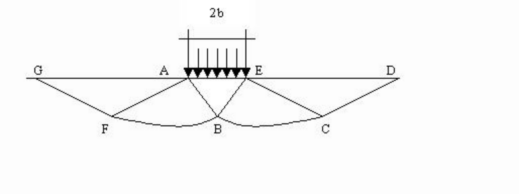
Identificand astfel volumul terenului adus la ruptura de sarcina limita, acesta poate fi calculat scriind conditia de echilibru dintre fortele agente pe orice volum de teren delimitat pe baza uneia dintre suprafetele de alunecare.
Se ajunge deci la o ecuatie q =B ´ c, unde coeficientul B depinde numai de unghiul de frecare j al terenului.
![]()
Pentru j =0 coeficientul B este egal cu 5.14, deci q=5.14 ´ c.
In celalalt caz particular de teren necoeziv (c=0, gą0) rezulta q= 0, dupa teoria lui Prandtl, nu ar fi posibil deci sa se aplice nicio sarcina pe suprafata limita a unui teren necoeziv.
De la aceasta teorie, chiar daca nu se aplica practic, au luat nastere cercetarile si metodele de calcul urmatoare.
De fapt Caquot s-a pus in aceleasi conditii ca si Prandtl exceptie facand faptul ca fasia de sarcina nu mai este aplicata pe suprafata semispatiului, dar la o adancime h, cu h Ł 2b; terenul dintre suprafata si adancimea h are urmatoarele caracteristici: gą0, j=0, c=0
si este deci un mediu care are greutate dar nu are rezistenta.
Rezolvand ecuatiile echilibrului se ajunge la expresia:
![]()
care, in mod sigur este un pas inainte fata de Prandtl, dar care inca nu oglindeste realitatea.
Metoda lui Terzaghi (1955)
Terzaghi , urmand studiul lui Caquot, a adus anumite modificari pentru a tine cont de caracteristicile efective ale cuplului lucrare de fundatie - teren.
Sub actiunea sarcinii transmisa de fundatie terenul care se gaseste in contact cu fundatia are tendinta de al aluneca lateral, dar este impiedicat de catre rezistentele tangentiale care se dezvolta intre fundatie si teren. Aceasta aduce cu sine o modificare a starii de tensiune in terenul de sub fundatie; pentru a tine seama de aceasta Terzaghi asigneaza laturilor AB si EB ale marginii lui Prandtl o inclinatie y fata de orizontala, alegand valoarea lui y in functie de caracteristicile mecanice ale terenului la contactul teren- fundatie.
Ipoteza g2 =0 pentru terenul de sub fundatie este depasita admitand ca suprafetele de ruptura raman nealterate, expresia sarcinii limita este deci:
![]()
in care C este un coeficient care rezulta in functie de unghiul de frecare j al terenului de sub suprafata de fundare si de unghiul j definit anterior;
b este semi-latimea fasiei.
Mai mult, bazandu-se pe date experimentale, Terzaghi trece de la problema plana la problema spatiala introducand factori de forma.
O contributie ulterioara afost adusa de Terzaghi asupra comportamentului efectiv al terenului.
In metoda lui Prandtl se presupune un comportament rigid-plastic al terenului, Terzaghi in schimb admite acest comportament in terenurile foarte compacte.
In aceste terenuri, curba sarcini-tasari prezinta o prima un parcurs rectiliniu, urmat de un parcurs scurt curbiliniu (comportament elastico-plastic); ruptura este instantanee si valoarea sarcinii limita este clar identificata (ruptura generala).
Intr-un tren foarte afanat in schimb, relatia sarcini-tasari prezinta un parcurs curbiliniu accentuat incepand de la sarcinile cele mai usoare cu un efect de ruptura progresiva a terenului (ruptura locala); in concluzie aflarea sarcinii limita nu este atat de clara si evidenta ca si in cazul terenurilor compacte.
Pentru terenurile foarte afanate, Terzaghi propune sa se ia in considerare sarcina limita, valoarea care se calculeaza cu formula precedenta introducand totusi valorile reduse ale caracteristicilor mecanice ale terenului si anume:
![]()
![]()
Explicând coeficientii formului precedente, formula lui Terzaghi poate fi scrisa:
![]()
unde:
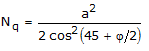
![]()
![]()

Formula lui Meyerhof (1963)
Meyerhof a propus o formula pentru calcularea sarcinii limita similara celei a lui Terzaghi; diferentele constau in introducerea unor coeficienti de forma ulteriori.
Acesta a introsus un coeficient sq care multiplica factorul Nq, factorii de adancime di si inclinatie ii pentru cazul in care sarcina transmisa fundatiei este inclinata pe verticala.
Valorile coeficientilor N au fost obtinuti de la Meyerhof ipotezand diferite arcuri de proba BF (v. mecanismul Prandtl) , in timp ce taierea de-a lungul planelor AF avea valori aproximate.
Factorii de forma aflati de catre Meyerhof sunt prezentati mai jos impreuna cu formula.
|
|
![]()
![]()
![]()
factor de forma:
|
pentru |
|
pentru |
factor de adâncime:
|
|
|
pentru |
|
pentru |
inclinatie:
|
|
|
pentru |
|
pentru |
unde :
![]()
θ = Inclinatia rezultantei pe verticala.
Formula lui Hansen (1970)
Este o exensie ulterioara a teoriei lui Meyerhof; extensiile constau in introducerea lui bi care tin cont de o eventuala inclinatie pe orizontala a suprafetei de fundare si un factor gi pentru terenul inclinat.
Formula lui Hansen este valabila pentru orice raport D/B, deci atat pentru fundatii superficiale cat si pentru cele de adancime, dar acelasi autor a introdus coeficientii pentru o interpretare mai buna a comportamentului real al fundatiei, fara de care ar fi crescut prea mult sarcina limita cu adancimea.
Pentru valori D/B <1
|
|
Pentru valori D/B>1:
|
|
In cazul φ = 0
------------------------------------------------------------------------------------------------------------------------
D/B 0 1 1.1 2 5 10 20 100
------------------------------------------------------------------------------------------------------------------------
d'c 0 0.40 0.33 0.44 0.55 0.59 0.61 0.62
------------------------------------------------------------------------------------------------------------------------.
In factorii urmatori expresiile cu (') sunt valabile cand j=0.
Factor de forma:
|
|
|
|
|
pentru fundatii continue |
|
|
|
Factor de adâncime:
|
||
|
||
|
||
|
pentru orice |
|
|
daca |
|
|
daca |
|
Factori de inclinatie a sarcinii:
|
|
|
|
|
|
|
|
|
|
Factori de inclinatie a terenului (fundatie pe versant):
|
|
|
Factori de inclinatie a planului de fundare (baza inclinata)
|
|
|
|
Formula lui Vesic (1975)
Formula lui Vesic este analoaga formulei lui Hansen, cu Nq si Nc ca pentru formula lui Meyerhof si Ng ca mai jos:
![]()
Factorii de forma si de adancime care apar in formulele de calcul a capacitatii portante sunt la fel cu cei propusi de Hansen; cateva diferente se inregistreaza in factorii de inclinatie a sarcinii, a terenului (fundatie sau versant) si a planului de fundare (baza inclinata).
Formula Brich-Hansen (EC 7 - EC 8)
Atat timp cat o fundatie poate rezista, sarcina de proiect cu masuri de siguranta in ceea ce priveste ruptura generala, pentru toate combinatiile de sarcina face referire la SLU (starea limita ultima), trebuie sa fie satisfacuta urmatoarea inegalitate:
![]()
Unde Vd este sarcina de proiect la SLU, normala la baza fundatiei, cuprinzand si greutatea fundatiei; in timp ce Rd este sarcina limita a proiectului fundatiei in relatie cu sarcinile normale, tinand cont si de efectul sarcinilor inclinate sau excentrice.
In calcularea analitica a sarcinii limita a proiectului Rd trebuiesc luate in considerare situatiile pe termen scurt si lung in terenurile cu granulatie mica.
Sarcina limita in conditii nedrenate se calculeaza ca:
![]()
unde
|
zona fundatiei eficace a proiectului, vazuta, in cazul sarcinii excentrice, ca si zona redusa pe centrul careia este aplicata la rezultanta sarcinii. |
cu |
coeziune nedrenata.
|
q |
presiune litostatica totala pe planul de fundare
|
sc |
factor de forma |
|
pentru fundatii rectangulare |
|
pentru fundatii patrate sau circulare. |
|
factor corector pentru inclinatia sarcinii datorata unei sarcini H. |
Pentru conditiile drenate sarcina limita de proiect este calculata dupa cum urmeaza:
![]()
Unde:
|
|
|
Factorii de forma
|
pentru forma rectangulara |
|
|
pentru forma patrata sau circulara |
|
|
pentru forma rectangulara |
|
|
pentru forma patrata sau circulara
|
|
|
|
Factori inclinatie rezultata datorata unei sarcini orizontale H paralela cu L’
|
|
Factori inclinatie rezultata datorata unei sarcini orizontale H paralela cu B’
|
|
|
In afara de factorii corectivi de mai sus sunt considerati aceia complementari adancimii planului de fundare si inclinatiei planului de fundare si a nivelului terenului. (Hansen).
Richards et. al.
Richards, Helm si Budhu (1993) au dezvoltat o procedura care permite, in conditii seismice, calcularea atat a sarcinii limita cat si a tasarilor induse, si deci calcularea ambelor stari limita (ultima si de deformatie). Calcularea sarcinii limita vine ca urmare a unei simple extensii a problemei sarcinii limita in cazul prezentei fortelor de inertie in terenul de fundare datorate seismului, in timp ce calcularea tasarilor se obtine prin abordarea lui Newmark (cfr. Apendice H din "Aspecte geotehnice ale proiectarii in zona seismica" - Asociatia Geotehnica Italiana). Autori au extins formula clasica trinomica a sarcinii limita:
![]()
Unde factorii de capacitate portanta sunt calculati cu urmatoarele formule:
![]()
![]()
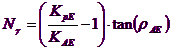
Examinand cu o abordare de echilibru limita, un mecanism de tip Coulomb si luand in comsiderare fortele de inertie ce actioneaza pe volumul de teren la ruptura. In camp static, mecanismul clasic al lui Prandtl poate fi aproximat dupa cum se vede in figura de mai jos, eliminand zona de tranzitie (evantaiul lui Prandtl) redusa doar la linia AC, care este considerata ca un zid ideal in echilibru sub actiunea impingerii active si a impingerii pasive primite de la penele I si III:
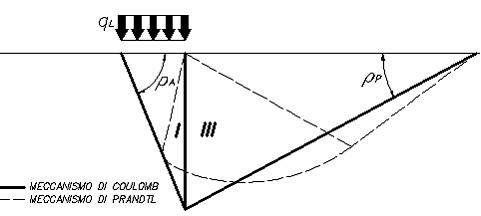
Schema de calcul a sarcinii limita (qL)
Autorii au obtinut expresiile unghiurilor ρA si ρP ce definesc zonele de impingere activa si pasiva, precum si a coeficientilor de impingere activa si pasiva KA si KP in functie de unghiul de frecare intern f al terenului si de unghiul de frecare d teren - zid ideal:
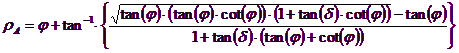


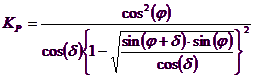
Trebuie oricum observat ca folosirea formulelor precedente luand ϕ=0.5δ , duce la valori ale coeficientilor de sarcina limita foarte apropiati celor bazati pe analiza de tip Prandtl. Richards et. al. au extins deci aplicarea mecanismului lui Coulomb la cazul seismic, tinand cont de fortele de inertie ce actioneaza pe volumul de teren la rupere. Aceste forte de masa, datorate acceleratiilor kh γ si kv γ , ce actioneaza in directie orizontala si verticala, sunt la randul lor egale cu kh γ si kv γ. Au fost obtinute astfel extensiile expresiilor lui ρa si ρp, precum si KA si KP, respectiv indicate ca ρAE si ρPE si ca KAE si KPE pentru denotarea conditiilor seismice.

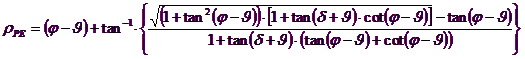
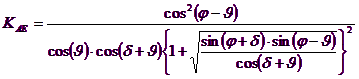
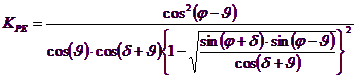
Valorile lui Nq si Nγ sunt determinabile folosind formulele precedente, implicand expresiile unghiurilor ρAE si ρPE si a coeficientilor KAE si KPE relative cazului seismic. In aceste expresii apare unghiul θ definit ca:
![]()
In tabela de mai jos sunt factorii de capacitate portanta calculati pentru urmatoarele valori ale parametrilor:
ϕ = 30°
δ = 15°
Si pentru diverse valori ale coeficientilor de impingere seismica:
kh/(1-kv) |
Nq |
Nγ |
Nc |
0 |
16.51037 |
23.75643 |
26.86476 |
0.087 |
13.11944 |
15.88906 |
20.9915 |
0.176 |
9.851541 |
9.465466 |
15.33132 |
0.268 |
7.297657 |
5.357472 |
10.90786 |
0.364 |
5.122904 |
2.604404 |
7.141079 |
0.466 |
3.216145 |
0.879102 |
3.838476 |
0.577 |
1.066982 |
1.103E-03 |
0.1160159 |
Tabelul factorilor de capacitate portanta pentru ϕ=30°
SARCINA LIMITA A FUNDATIILOR IN ROCA
Pentru aflarea capacitatii portante admisibila a rocilor trebuie sa se ia in considerare anumiti parametri semnificativi printre care caracteristicile geotehnice, tipul de roca si calitatea acesteia masutrata cu RQD. In capacitatea portanta a rocilor se folosesc in mod normal factori de siguranta ridicati si care au legatura cu coeficientul RQD: de exemplu, pentru o roca cu RQD egal cu maxim 0.75 factorul de siguranta variaza intre 6 si 10. Pentru determinarea capacitatii portante a unei roci se pot folosi formulele lui Terzaghi, utilizand ungiul de frecare si coeziunea rocii, sau cele propuse Stagg si Zienkiewicz (1968) in care coeficientii formulei capacitatii portante sunt:
|
|
|
Cu acesti coeficienti se folosesc factorii de forma din formula lui Terzaghi.
Capacitatea portanta ultima calculata si fuziunea coeficientului RQD dupa expersia:
![]()
In cazul in care carotajul din roca nu furnizeaza bucati intacte (RQD tinde spre 0), roca este tratata ca un teren estimand parametrii c si ϕ.
VERIFICAREA LA ALUNECARE
In conformitate cu criteriile proiectului la SLU, stabilitatea unuei fundatii izolate trebuie sa fie verificata in functie de colapsul prin alunecare pe langa cel de ruptura generala. In comparatie cu colapsul prin alunecare rezistenta se calculeaza ca suma a unei componente datorata aderentei si una datorata forfecarii fundatie-teren; rezistenta laterala care deriva din impingerea pasiva a terenului poate fi luata in considerare in functie de un procent stabilit de catre utilizator.
Rezistenta de calcul pentru forfecare si adeziune se calculeaza conform expersiei:
FRd = Nsd tanδ+ca A’
In care Nsd reprezinta valoarea de calcul a fortei verticale, δ si unghiul de rezistenta la taiere la baza fundatiei izolate, ca reprezinta aderenta fundatie-teren si A’ este suprafata fundatiei eficace, inteleasa, in cazul sarcinilor excentrice, ca si suprafata redusa la centrul careia este aplicata rezultanta.
Tasarile unei fundatii rectangulare de dimensiunea BXL situata pe suprafata unui semispatiu elastic se pot calcula in baza unei ecuatii bazata pe teoria elasticitatii (Timoshenko si Goodier (1951)):
|
(1-2) |
unde:
q0 = Intensitatea presiunii de contact.
B' = Minima dimensiune a ariei care reactioneaza.
E si μ = Parametrii elastici ai terenului.
Ii = Coeficientii de influenta dependenti de : L'/B', grosimea stratului H, coeficientul lui Poisson μ, adâncimea planului de fundare D.
Coeficientii I1 si I2 se pot calcula utilizand ecuatiile date de Steinbrenner (1934) (V. Bowles), in functie de raportul L'/B' ed H/B, utilizand B'=B/2 e L'=L/2 pentru coeficientii relativi la centru si B'=B si L'=L pentru coeficientii realtivi la margine.
Coeficientul de influenta IF deriva din ecuatiile lui Fox (1948), care indica tasarea, se reduce cu adancimea in functie de coeficientul lui Poisson si de raportul L/B.
Pentru simplificarea ecuatiei (1) se introduce coeficientul IS:
![]()
Tasarea stratului de grosimea H:
![]()
Pentrui a aproxima mai bine tasarile se subdivide baza de rezemare astfel incat punctul sa se gaseasca in corespondenta cu un unghi extern comun mai multor dreptunghiuri. In pratica se multiplica cu un factor egal cu 4 pentru calculul tasarilor la centru si cu un factor egal cu 1 pentru tasarile la margine.
In calcularea tasarilor se considera o adancime a bulbului tensiunilor egala cu 5B, daca substratul de roca se gaseste la o adancime mare.
In acest sens se considera substrat de roca stratul care are valoarea lui E egala cu de 10 ori mai mult grosimea stratului de deasupra.
Modulul elastic pentru terenuri stratificate se calculaaza ca medie ponderata a modulelor elastice ale stratelor supuse tasarii imediate.
Calculul tasarilor cu metoda edometrica da posibilitatea calcularii tasarii de consolidare de tip monodimensional, produsa de tensiuni induse de o sarcina aplicata in conditii de expansiune laterala impiedicata. Deci, estimarea efectuata cu aceasta metoda este considerata mai mult empirica decat teoretica.
Asadar usurinta folosirii si facilitatea controlarii influentei variilor diversilor parametri care intervin in calcul, fac din aceasta o metoda larg folosita.
Metoda edometrica a calcularii tasarilor trece prin doua faze:
| a. | calcularea tensiunilor verticale induse la diferite adancimi cu aplicarea teoriei elasticitatii ; |
| b. | calcularea parametrilor de copresibilitate prin incercarea edometrica |
In ceea ce priveste rezultatele incercarii edometrice, tasarea este calculata ca:
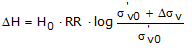
daca avem de-a face cu un teren supraconsolidat (OCR>1), sau daca cresterea tensunii datorata aplicarii sarcinii nu creste presiunea de preconsolidare σ’p (![]() <σ’p).
<σ’p).
Daca insa terenul nu este normalconsolidat (s’vo=s’p) deformarile apar la compresiune iar tasarea se calculeaza ca:
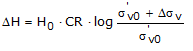
unde:
RR Rapoart de recompresiune;
CR Raport de compresiune;
H0 grosimea initala a stratului;
σ’v0 tensiunea verticala efectiva inainte de aplicarea sarcinii.
Δσv cresterea tensiunii verticale la aplicarea sarcinii.
In alternativa la parametrii RR si CR se face referire la modulul edometric M; in acest de caz trebuie sa se alega potrivit valoarea modulului de utilizat, tinand cont de intervalul de tensiune (![]() ) semnificativ pentru problema.
) semnificativ pentru problema.
Aplicarea corecta a acestei metode cere:
| • | subdivizarea stratelor compresibilie intr-o serie de strate de grosime mica (< 2.00 m); |
| • | estimarea modulului edometric pentru fiecare strat; |
| • | calculul tasarilor ca suma a contribitiei fiecarui strat mic in care a fost divizat blocul compresibil. |
Multi folosesc expresiile de mai sus pentru calcularea tasarii de consolidare atat pentru argile cat si pentru nisipuri de granulatie de la fina la medie, deoarece modulul de elasticitate folosit este extras direct din incercarile de consolidare. Totusi, pentru terenuri cu granulatie mai mare dimensiunile incercarilor edometrice sunt putin semnificative fata de comportamentul global al stratului iar pentru nisipuri este de preferat incercarea de penetrometie statica sau dinamica.
TASAREA SECUNDARA
Tasarea secundara este calculata cu:
![]()
in care
Hc reprezinta inaltimea stratului in faza de consolidare;
Ca este coeficientul de consolidare secundara ca inclinatiei in partea secundara a curbei tasare- logaritm timp;
T timpul pentru care se calculeaaza tasarea secundara;
T100 timpul necesar epuizarii procesului de consolidare primara.
METODA LUI SCHMERTMANN
O metoda alternativa pentru calculul tasarilor este cea propusa de Schmertmann (1970) care se coreleaza variatia bulbului tensiunilor cu deformatia. Schmertmann a propus deci considerarea unei diagrame a deformarilor de forma triunghiulara in care adancimea la care exista deformatii semnificative este 4B, in cazul fundatiilor continue, si egala cu 2B pentru fundatii patrate sau circulare.
Conform aceastei abordari tasarea se exprima prin intermediul expresiei:
![]()
in care:
Dq reprezinta sarcina neta aplicata fundatiei;
Iz este un factor de deformare a carui valoare este nula la adancimea 2B, pentru fundatia circulara sau patrata, si la adâncimea 4B, pentru fundatiile continue.
Valoarea maxima a lui Iz se verifica la o adâncime agala cu:
B/2 pentru fundatiile patrate sau circulare
B pentru fundatiile continue

unde σ’vi reprezinta tensiunea verticala efectiva la adancimea B/2 pentru fundatii patrate sau circulare, si la adancimea B pentru fundatii continue.
Ei reprezinta modulul de deformatie al terenului corespunzator stratului i considerat in calcul;
Δzi reprezinta grosimea stratului i;
C1 e C2 sunt doi coeficienti de corectie.
Modulul E este considerat egal cu 2.5 qc pentru fundatii circulare si patrate si cu 3.5 qc pentru fundatii continue. In cazurile intermediare se interpoleaza in functie de valoarea lui L/B.
Termenul qc care intervine in determinarea lui E reprezinta rezistenta la varf data de incercarea CPT.
Expresiile celor doi coeficienti C1 si C2 sunt
|
care tine cont de adancimea planului de fundare. |
|
care tine cont de deformatiile diferite in timp prin efect secundar. |
In expresie t reprezinta timpul exprimat in ani dupa terminarea constructiei, in corespondenta cu care se calculeaza tasarile.
METODA LUI BURLAND SI BURBIDGE
Atunci cand se dispune de datele obtinute pentru incercarile de penetrometrie dinamica pentru calculul tasarilor este posibila apelarea la metoda lui Burland si Burbidge (1985), in care este corelat un indice de compresibilitate Ic rezultatuli N al incercarii de penetrometrie dinamica. Formula tasarii propusa de cei doi este:
![]()
in care:
q' = presiunea eficace bruta;
σ'vo = tensiunea verticala eficace la cota fundatiei;
B = latimea fundatiei;
Ic = indice de compresibilitate;
fs, fH, ft = factorii corectivi care tin cont de forma, de grosimea stratului compresibil si de timp, pentru componenta vascoasa.
Indicele de compresibilitate Ic este legat de valoarea medie Nav a lui Nspt in interiorul unei adancimi semnificative z:
![]()
In ceea ce priveste valorile Nspt de utilizat in calcul de valoarii mediei NAV - este de precizat ca vaolorile trebuie sa fie corectate, pentru nisipuri cu componenta prafoasa sub panza freatica Nspt>15, dupa indicatia lui Terzaghi si Peck (1948)
![]()
unde Nc este valoarea corectata de folosit in calcule.
Pentru depozite de pietris sau nisipoase-pietroase valoare corectata este egala cu :
![]()
Expresiile factorilor de corectie fs, fH si ft sunt:
|
|
|
Cu
t = timpul in ani > 3;
R3 = costanta egala cu 0.3 pentru sarcini statistice si 0.7 pentru sarcini dinamice;
R = 0.2 in cazul sarcinilor statice si 0.8 pentru cele dinamice.
Metoda lui Seed si Idriss (1982) este cea mai cunoscuta si utilizata dintre metodele simplificate si solicita cunoasterea doar a câtorva parametrii geotehnici: granulometria, numarul de lovituri in incercarea SPT, densitatea relativa, greutatea volumica. Pentru a determina valoarea coeficientului reductiv rd este utlizata formula empirica propusa de Iwasaki et al. (1978):
![]()
in timp ce pentru factorul de corectie MSF consultati tabelul 1 unde este afisata valoarea acestui factor obtinut de diversi cercetatori, printre care Seed H.B. si Idriss I.M. (1982).
Tabelul 1 - Magnitudine Scaling Factor
Magnitudine |
Seed H. B. & Idriss I. M. (1982) |
5.5 6.0 6.5 7.0 7.5 8.0 8.5 |
1.43 1.32 1.19 1.08 1.00 0.94 0.89 |
Rezistenta la lichefiere CRR este calculata in functie de magnitudine, de numarul de lovituri, presiune verticala efectiva, densitate relativa.
Se obtine un grafic (Fig. 1) selectionând cazurile de terenuri in care a existat lichefiere si in care nu a existat lichefiere in timpul cutremurelor.
Se calculeaza initial numarul de lovituri corect la cota dorita pentru a tine cont de presiunea litostatica cu ajutorul urmatoarei expresii:
![]()
unde:
Nm este numarul de lovituri in incercarea penetrometrica standard SPT;
CN este un coeficient corectiv ce se calculeaza cu ajutorul urmatoarei expresii:

unde:
s'vo este presiunea verticala efectiva;
Pa presiunea atmosferica exprimata in aceleasi unitati ca si s'vo;
n un exponent ce depinde de densitatea relativa a terenului (Fig. 2).
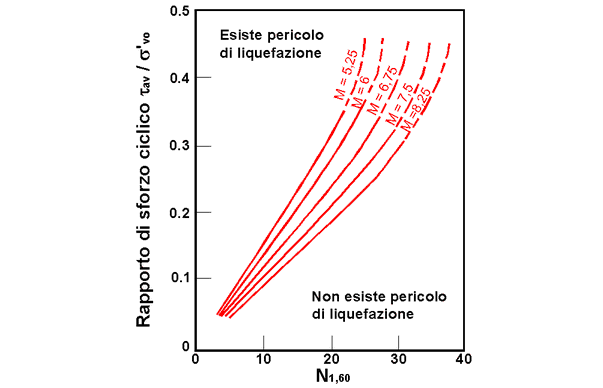
Figura 1 – Corelatia dintre CSR si N1.60.
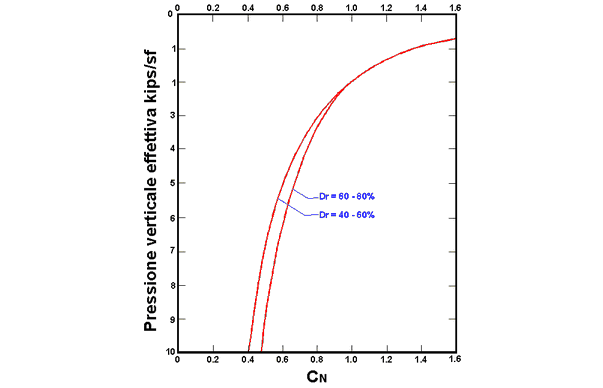
Figura 2 – Coeficient corectiv CN
S-a demonstrat ca pentru un cutremur cu magnitudine de 7,5 CRR este:
![]()
Se aplica deci:
![]()
daca FS > 1,3 depozitul nu este lichefiabil.
Autorii au precizat ca aceasta procedura este valida pentru nisipuri cu D50 > 0.25 mm; pentru nisipuri argiloase si argile sugereaza sa se corecteze ulterior valoarea lui N1,60:
![]()
© 2015 GeoStru Software