Lo studio del trasporto solido per trascinamento di fondo prende le mosse dall’analisi della condizione di inizio moto delle particelle solide disposte sul fondo dell’alveo. Lo studio di questa condizione di “equilibrio limite”, denominata di moto incipiente , può essere condotta facendo ricorso a equazioni in cui figura la tensione critica di trascinamento.
La rappresentazione del fenomeno del trasporto solido di fondo, proposta da Shields si fonda sulla teoria della turbolenza . Le ipotesi che stanno alla base della deduzione della condizione di equilibrio limite sono:

· La spinta esercitata dalla corrente su una particella solida è proporzionale alla superficie investita, che dipende dal quadrato del diametro e dal quadrato della velocità.

· La forza resistente dipende esclusivamente dalla forma del fondo alveo (alveo piano, scabrezza assoluta rappresentata dal diametro delle particelle).

Sulla base delle precedenti ipotesi e nel caso di fondo orizzontale e granulometria dei sedimenti uniforme , lo stato fisico di incipiente movimento è espresso dal seguente legame funzionale:

Che nella condizione idraulica di microscabrezza (h/d ³ 6)si semplifica nell’espressione:

La forma funzionale dell’espressione precedente, determinata sperimentalmente da Shields, è rappresentata in Figura ed è nota come Abaco di Shields.

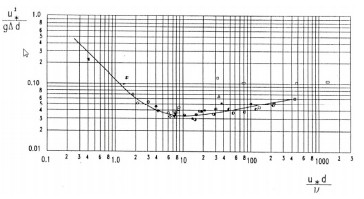
Abaco di Shields

Alcuni autori, partendo dall’esperienza di Shields e rimuovendo i limiti sperimentali sopra discussi sono riusciti a calibrare delle equazioni applicabili anche in condizioni di : granulometria non uniforme, bassi valori del grado di sommergenza, fondo dell’alveo inclinato, forma della sezione..
Sono di seguito elencati alcuni possibili abbinamenti per le formule di trasporto e di incipiente movimento, è opportuno, quando possibile, utilizzare formule fra loro omogenee dal punto di vista concettuale e della fonte (ovvero dei dati su cui sono state tarate), al fine di minimizzare la dispersione del risultato.

In alcune delle seguenti formule verrà introdotta la portata solida volumetrica adimensionalizzata Φ che ha la seguente espressione:

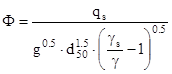
Schocklitsch (1962)

ρ_s [kg/m³] densità del sedimento

ρ_w [kg/m³] densità dell’acqua

i pendenza del fondo alveo

g [m/s²] accelerazione di gravità

q [m³/(s·m)] portata liquida per unità di larghezza

q_s [m³/(s·m)] portata solida volumetrica per unità di larghezza

q_c [m³/(s·m)] portata critica

d₅₀[m] diametro medio dei sedimenti dell’alveo

Bathurst et al. (1987)- Meyer-Peter e Müller modificato

g_s [kg/m³] peso dell’unità di volume del sedimento

g_w [kg/m³] peso dell’unità di volume dell’acqua

Φ portata solida volumetrica adimensionalizzata
ϕ^c₀ valore critico del numero di Shields

i pendenza del fondo alveo

d₅₀[m] diametro medio dei sedimenti dell’alveo
h [m] altezza di moto uniforme
t [kg/m²] tensione di trascinamento della corrente

Meyer-Peter e Müller (1948)

L’equazione è stata calibrata dagli autori utilizzando materiali a granulometria non uniforme (diametro medio variabile tra 0.4mm e 29 mm), valori della pendenza del canale sperimentale variabile tra 0.0004 e 0.02, densità del sedimento compresa tra 1.25 e 4 g/cm³, altezza del pelo libero della corrente compresa tra 0.15 e 2 m.

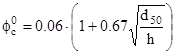
g_s [kg/m³] peso dell’unità di volume del sedimento

g_w [kg/m³] peso dell’unità di volume dell’acqua

Φ portata solida volumetrica adimensionalizzata
ϕ^c₀ valore critico del numero di Shields

i pendenza del fondo alveo

d₅₀[m] diametro medio dei sedimenti dell’alveo
h [m] altezza di moto uniforme
t [kg/m²] tensione di trascinamento della corrente
θ [°] inclinazione del fondo alveo
β [°] angolo di attrito dei sedimenti

Suszka (1991)
Valida per granulometria del sedimento non uniforme (3.3-43.5 mm), grado di sommergenza compresa tra 0.9 e 73.3, pendenza media del canale compresa tra 0.0017 e 0.09, numero di Renoilds [147, 14000].

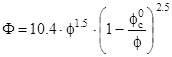
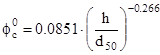
g_s [kg/m³] peso dell’unità di volume del sedimento

g_w [kg/m³] peso dell’unità di volume dell’acqua

Φ portata solida volumetrica adimensionalizzata
ϕ^c₀ valore critico del numero di Shields

i pendenza del fondo alveo

d₅₀[m] diametro medio dei sedimenti dell’alveo
h [m] altezza di moto uniforme
t [kg/m²] tensione di trascinamento della corrente

Smart & Jaggi (1983)

L’espressione è stata ricavata utilizzando i dati sperimentali di Meyer-Peter e Müller e ulteriori dati ottenuti da prove con pendenza del fondo alveo compresa nell’intervallo 0,03-0,2 e rapporto d₉₀/d₃₀ ≤ 10. L'equazione utilizzata è la seguente:

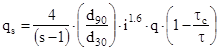
s (r_s/r_w) rapporto tra la densità dei sedimenti e quella dell’acqua

i pendenza del fondo alveo

q [m³/(s·m)] portata liquida per unità di larghezza

q_s [m³/(s·m)] portata solida volumetrica per unità di larghezza

t_c [kg/m²] tensione critica di Shields

d₅₀[m] diametro medio dei sedimenti dell’alveo
d₉₀[m] diametro corrispondente al 90% di passante

Rickenmann (1990)

Si applica generalmente per pendenze del fondo alveo comprese tra 0.05-0.2 e rapporto d₉₀/d₃₀ ≤ 10..

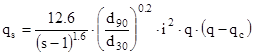
dove:

s (r_s/r_w) rapporto tra la densità dei sedimenti e quella dell’acqua

i pendenza del fondo alveo

g [m/s²] accelerazione di gravità

q [m³/(s·m)] portata liquida per unità di larghezza

q_s [m³/(s·m)] portata solida volumetrica per unità di larghezza

q_c [m³/(s·m)] portata critica

d₉₀[m] diametro corrispondente al 90% di passante
d₅₀[m] diametro corrispondente al 50% di passante
d₃₀[m] diametro corrispondente al 30% di passante