Moment de cedare piloti

Calculul momentului de plasticizare pentru o sectiune tubularã din otel

Sectiunea luatã în considerare este urmãtoarea:

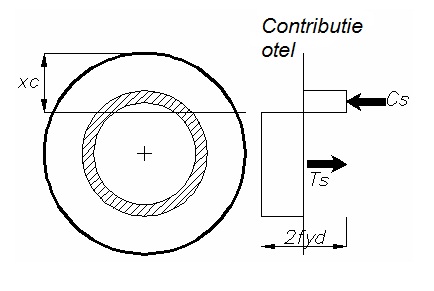
contributie otel

Schema pentru momentul de plasticizare al unei sectiuni tubulare din otel

Calculul momentului de plasticizare a fost efectuat presupunând, pentru otel, o legãturã constitutivã de tip rigid plastic, cu tensiune limitã de curgere egalã cu fyd. Momentul de plasticizare a fost determinat prin interpolarea pe curba de interactiune a sectiunii.

Pentru construirea curbei de interactiune a sectiunii s-a urmat procedura de mai jos:

-	pas 1 - se fixeazã adâncimea axei neutre (xc) - (plecând de la xc = 0);

-	pas 2 - calculul rezultantei în termeni de efort normal (Nd);

-	pas 3 - calculul momentului rezultant (Md), fatã de baricentru geometric al sectiunii;

-	pas 4 - memorarea punctului calculat (Nd, Md);

-	pas 5 - Increment xc, dacã xc este mai mic sau maximegal cu diametrul sectiunii atunci ne întoarcem la pasul 1, altfel procesul este încheiat.

Notã:

În acest mod se construieste partea superioarã a domeniului de interactiune. Partea inferioarã este identicã, dar antisimetricã.

Un punct generic al domeniului de interactiune a fost calculat cu formulele de mai jos:

În formulele precedente simbolurile au urmãtoarele semnificatii:

-	Ac_s - Aria de otel comprimat;

-	At_s - Aria de otel întins;

-	fcd - Rezistenta de calcul beton;

-	fyd - Rezistenta de calcul otel;

-	dCs - Distanta între rezultanta tensiunilor în compresiune a otelului si baricentrul sectiunii;

-	dTs - Distanta între rezultanta tensiunilor la întindere a otelului si baricentrul sectiunii;

Calculul momentului de plasticizare pentru o sectiune tubularã din otel imersã într-o sectiune circularã de beton

Formula precedentã, utilizatã pentru sectiunea tubularã, poate fi extinsã la cazul în care tubul este imers într-o sectiune din beton. În acest caz este nevoie sã se tinã cont de contributia betonului, conform schemei de mai jos:

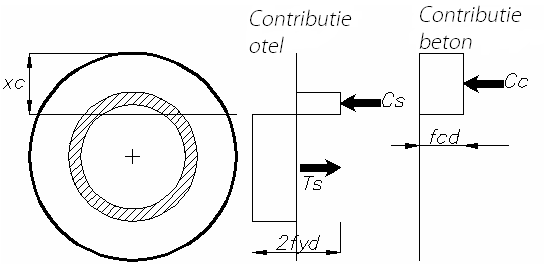
Schema pentru momentul de plasticizare al unei sectiuni tubulare din otel imersã într-o sectiune circularã din beton

Dupã cum se poate observa, betonul este considerat reactiv si doar cel comprimat. Valoarea solicitãrilor corespunzãtoare unei adâncimi fixate a axei neutre a sectiunii este:

În formulele precedente simbolurile au urmãtoarele semnificatii:

-	Ac_s - Aria de otel comprimat;

-	Ac_c - Aria de beton comprimat;

-	At_s - Aria de otel întins;

-	fcd - Rezistenta de calcul beton;

-	fyd - Rezistenta de calcul otel;

-	dCs - Distanta între rezultanta tensiunilor în compresiune a otelului si baricentrul sectiunii;

-	dCc - Distanta între rezultanta tensiunilor în compresiune a betonului si baricentrul sectiunii;

-	dTs - Distanta între rezultanta tensiunilor la întindere a otelului si baricentrul sectiunii;

Calculul momentului de plasticizare pentru o sectiune circularã din B.A.

Si în acest caz se presuoune o legãturã constitutivã a materialelor de tip rigid plastic, cu tensiuni limitã egale cu fcd si fyd, respectiv pentru beton si pentru otel. Schema de referintã este:

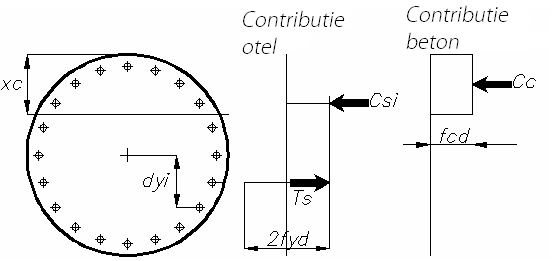
Schema de referintã pentru calculul momentului de plasticizare a unei sectiuni circulare din B.A.

În acest caz, valoarea solicitãrilor, în corespondentã cu o adâncime prefixatã a axei neutre este urmãtoarea:

În formulele precedente simbolurile au urmãtoarele semnificatii:

-	Ac_c - Aria de otel comprimat;

-	Asi+ - Aria barei de armãturã i, ce se aflã deasupra axei neutre;

-	Asi- - Aria barei de armãturã i, ce se aflã sub axa neutrã;

-	Asi - Aria barei de armãturã i;

-	fcd - Rezistenta de calcul beton;

-	fyd - Rezistenta de calcul otel;

-	dCc - Distanta între rezultanta tensiunilor în compresiune a betonului si baricentrul sectiunii;

-	dyi - Distanta pozitivã (de-a lungul verticalei) mãsuratã între baricentru barei de armaturã i si baricentrul sectiunii;