
|

|
Atentie, pentru calculul suprapresiunilor interstitiale trebuie asignate datele aditionale în Caracteristici geotehnice.
Presiuni interstitiale dupã seism Pentru calcularea presiunilor interstitiale dupã seism asignati coeficientilor seismici orizontali si verticali 0, iar acceleratiei seismice o valoare diferitã de zero.
|
Rezistenta la forfecare în conditii de sarcinã seismicã.
În lipsa unor determinãri experimentale adecvate, obtinute din încercãri ciclice de laborator, reducerea rezistentei de forfecare în conditii de sarcinã seismicã poate fi calculatã folosind relatii empirice de citire, dupã cum este indicat în paragrafele de mai jos, cu referire la cazul analizelor conduse în termeni de tensiuni efective sau de tentiuni totale.
Analiza în conditii de tensiuni efective.
Incrementul presiunii interstitiale trebuie calculat în cazul terenurilor saturate dacã deformarea la forfecare indusã de actiunea seismicã este superioarã valorii deformãrii pragului volumetric, gv. În terenuri partial saturate, presiunea interstitialã reste în timpul aplicãrii solicitãrii seismice, dar se mentine în general inferioarã presiunii atmosferice; în acest caz poate fi luatã o valoare nulã a presiunilor interstitiale pentru toatã perioada de aplicare a sarcinii (s’=s) iar dacã analizele pot fi realizate utilizând caracterisiticle de rezistentã dererminate în încercãri drenate realizate pe specimene saturate ale aceluiasi material. Pentru calculul lui Du trebuie fãcutã distinctie între comportamentele terenurilor în functie de natura lor diferitã, coezivã sau necoezivã.
Terenuri coezive.
Pentru terenurile coezive, incrementul de presiune interstitialã Du, la o anumitã adâncime, poate fi calculat cu ajutorul urmãtoarei relatii empirice (Matsui et al., 1980):
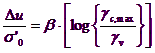
Unde s’0 este valoarea initialã a presiunii medii efective la adâncimea consideratã, gc,max este deformarea de forfecare maximã atinsã în timpul seismului iar b=0.45 este un coeficient experimental. Deformarea pragului volumetric gv, determinabil cu încercãri ciclice de laborator, poate fi calculat într-o primã aproximare cu ajutorul formulei:
![]()
În care OCR este gradul de supraconsolidare, A si B sunt coeficienti experimentali care, în absenta unei determinãri directe, pot fi calculati în functie de indicele de plasticitate:
Ip(%) |
A |
B |
|---|---|---|
20 |
0.4 10-3 |
0.6 10-3 |
40 |
1.2 10-3 |
1.1 10-3 |
55 |
2.5 10-3 |
1.2 10-3 |
Valori sugerate pentru coeficientii A si B
Valoarea lui gc,max relativ la adâncimea consideratã poate fi determinat prin intermediul unei analize a rãspunsului seismic local. Altfel, se determinã preliminar valoarea lui tmax cu ajutorul formulei empirice:
![]()
Unde amax, exprimatã în g, este acceleratia maximã la nivelul terenului pe verticala relativã punctului considerat; g este acceleratia gravitationalã; sv este tensiunea verticalã totalã; rd este un coeficient reductiv ce tine cont de actiunea seismicã la adâncimea de interes care aduce în discutie deformabilitatea subsolului. Coeficientul rd poate fi calculat, ca primã aproximare, cu expresia de mai jos:
![]()
Unde z este adâncimea în punctul considerat. Deformarea maximã de forfecare indusã de seism se calculeazã deci cu formula:
![]()
Unde modulul de forfecare G poate fi determinat, iterativ, de curba (G-γ) obtinutã din încercãri de laborator.
Terenuri granulare.
În terenurile granulare incrementul presiunii interstitiale generat de solicitarea seismicã poate fi calculat cu urmãtoarea formulã empiricã (Seed & Booker, 1997):
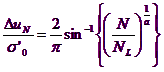
Unde Dun este incrementul de presiune interstitialã dupã N cicluri de sarcinã, s'0 este valoarea initialã a presiunii medii efective la adâncimea consideratã, N este numãrul de cicluri de sarcinã de amplitudine constantã echivalentã seismului iar NL este numãrul de cicluri de sarcinã necesare pentru producerea lichefierii în teren. Constanta experimentalã a poate fi calculatã cu relatia propusã de Fardis & Veneziano (1981) în functie de densitatea relativã Dr (în fractie):
![]()
Termenul εq are distributie log-normalã cu valoare medie unitarã si variatie egalã cu 0.1. Pentru determinarea numãrului de cicluri N ce apare în una dintre relatiile anterioare este necesarã aproximarea deformãrilor de forfecare neregulate induse de cutremur cu o solicitare ciclicã echivalentã de amplitudine constantã (teq) si numãr de cicluri echivalent (Neq) urmând una dintre numeroasele proceduri prezente în literaturã. Utilizând de exemplu procedura propusã de Biondi et al. (2004) se obtine:
![]()
![]()
În prima dintre ecuatiile precedente tmax reprezintã solicitarea de forfecare maximã indusã de teren la adâncimea consideratã, a cãrei valori poate fi caclulat cu ajutorul unei analize a rãspunsului seismic local sau, la o primã aproximare, cu ajutorul unei formule utilizatã în paragraful referitor la terenuri coezive. În a doua ecuatie din cele precedente diversii termeni au urmãtoarele semnificatii:
| - | Ia - intensitatea lui di Arias (m/s); |
| - | v0 - intensitatea intersectiilor cu axa timpilor accelerogramei (s-1); |
| - | TD - durata accelerogramei definitã de Trifunac si Brady (s); |
Intensitatea lui Arias este definitã prin formula de mai jos:
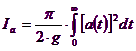
Celelalte simboluri care apar, α -β -γ - δ - ε, sunt constante pentru care se sugereazã valorile:
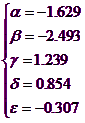
Pentru determinarea valorii lui NL se poate face referire la metodele ce se bazeazã pe interpolãri de tip grafic sau eventual pe utilizarea rezultatelor din încercãri triaxiale ciclice sau de forfecare simplã ciclicã.
|
© GeoStru Software