Calculul impingerii active cu metoda lui Coulomb se bazeaza pe studiul echilibrului limita global al sistemului foramt din zid si prismul de teren din spatele lucrarii in cazul unei suprafete cu asperitati.

Pentru teren omogen si uscat diagrama presiunilor este liniara avand distributia:

 

 

Impingerea St este aplicata la 1/3 H din valoare:

Fiind indicata cu:

 

 

 

 

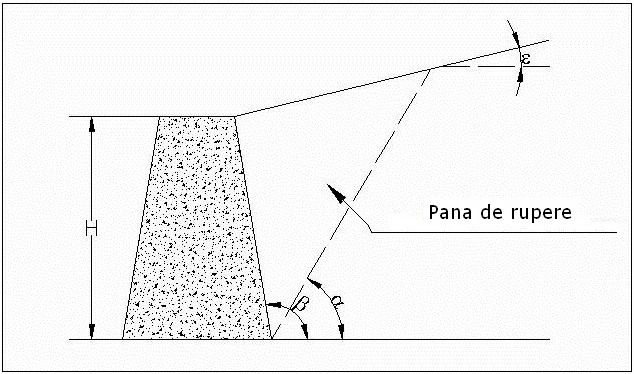
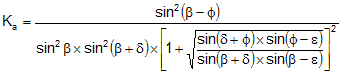
Valori limita KA:

δ < (β-ϕ-ε) dupa Muller-Breslau

 

 

 γt = Greutatea volumica a terenului;

 β = inclinatie a peretelui intern fata de orizontala care trece prin talpa;

 ϕ = Unghiul de rezistenta la forfecare al terenului;

 δ = Unghi de forfecare teren-zid;

 ε = inclinatia campului fata de orizontala, pozitiva daca este in sens invers acelor de ceasornic;

 H = inaltimea peretelui.

 

 

Calculul impingerii active dupa Rankine

 

Si e = d = 0 e b = 90° (zid cu perete vertical neted si terasament cu suprafata orizontala) impngerea St se simplifica de forma:

 

 

 

care coincide cu ecuatia lui Rankine pentru calculul impingerii active a terenului cu terasament orizontal.

Rankine a adoptat in pincipiu aceleasi ipoteze facute de Coulomb, cu exceptia faptului ca a ignorat frecarea teren-zid si prezenta coeziunii. In formularea sa generala expresia lui Ka se prezinta ca:

 

 

 

 

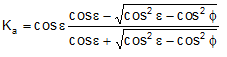
Calcularea impingerii active cu metoda lui Mononobe & Okabe

 

Calcularea impingerii active cu metoda Mononobe & Okabe priveste evaluarea impingerii in conditii seismice cu metoda pseudo-statica. Aceasta se bazeaza pe studierea echilibrului limita global al sistemului format din zid si prisma de teren omogen din spatele lucrarii care participa la ruptura intr-o configuratie artificiala de calcul in care unghiul e, de inclinatie a campului fata de planul orizontal, si unghiul b de inclinatie a peretelui intern fata de planul orizontal care trece prin talpa, sunt marite cu o cantitate q unde:

 

tg θ = kh/(1±kv)

 

cu kh coeficient seismic orizontal si kv vertical.

in absenta studiilor specifice, coeficientii kh si kv trebuiesc calculati:

 

               kh = S⋅ag/r                 kv = 0,5 kh

 

in care Sag reprezinta valoarea de acceleratie seismica maxima a terenului pentru variatele categorii de profil stratigrafic.Factorului r ii poate fi desemnata valoarea  r = 2 in cazul lucrarilor destul de flexibile (ziduri de greutate), in timp ce in toate celelalte cazuri i se da valaorea 1 (ziduri in b.a. rezistenti la flexie, ziduri in b.a. pe piloti sau ancoraje, ziduri de inchidere).

 

 

Efectul datorat coeziunii

Coeziunea induce presiuni negative constante egale cu:

 

 

Nefiind posibila stabilirea a priori care este reducerea indusa in impingere prin efectul coeziunii, a fost calculata o inaltime critica Zc in felul urmator:

 

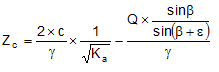
unde:

 

Q = incarcare agenta pe rambleu;

 

Daca Zc<0 este posibila suprapunerea directa a efectelor, cu o reducere egala cu:

 

Zc = Pc × H

 

cu punctul de aplicare egal cu H/2;

 

Sarcina uniforma pe terasament

O incarcare Q, uniform distribuita pe rambleu induce presiuni constante egale cu:

 

Pq = KA×Q×senβ/sen(β+ε)

 

Pentru integrare, o impingere egala cu Sq:

 

Cu punct de aplicare la H/2, avand notat cu Ka coeficentul de impingere active conform Muller-Breslau.

 

Impingerea activa in conditii seismice

In prezenta seismicitatii forta de calcul exercitata de rambleu asupra zidului este data de:

 

 

unde:

 

H = inaltimea zidului;

kv = coeficientul seismic vertical;

γ = greutatea volumica a terenului;

K = coeficienti de impingere activa totala (satatica + dinamica);

Ews = impingere hidrostatica a apei;

Ewd = impingere hidrodinamica.

 

Pentru terenuri impermeabile impingerea hidrodinamica Ewd = 0, dar se efecueaza o corectie asupra evaluarii unghiului  q a formulei Mononobe & Okabe dupa cum urmeaza:

 

 

in terenurile cu permeabilitate ridicata in conditii dinamice continua sa se aplice corectia de mai sus, dar impingerea hidrodinamica ia forma:

 

 

Cu H’ inaltimea nivelului panzei freatice masurata plecand de la baza zidului.

 

Impingerea hidrostatica

Panza freatica cu suprafata situata la o distanta Hw de la baza zidului induce presiuni hidrostatice normale peretelui care, la adancimea z, se exprima astfel:

Pw(z) = γw × z

 

Cu rezultantele egale cu:

Sw = 1/2 × γw× H²

 

 

impingerea terenului imers se obtine inlocuind gt cu g't (g't = gsaturat - gw), greutate eficace a materialului imers in apa.

 

 

Rezistenta pasiva

Pentru teren omogen diagrama presiunilor este  liniara de tipul:

 

Pt = Kp× γt× z

 

pentru integrare se obtine impingerea pasiva:

 

 

Indicand cu:

 

 

 

 

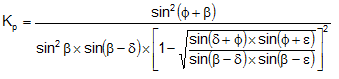
(Muller-Breslau) cu valori limita ale lui d egale cu:

 

δ< β-ϕ-ε

 

Expresia lui Kp dupa formularea lui Rankine ia urmatoarea forma:

 

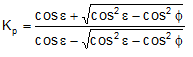
©    GeoStru Software